1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
| clear; clc;
damping_ratios = [ 0.01, 0.02, 0.05, 0.10];
T = linspace(0.01, 10, 1000);
dt = 0.005;
g = 9.81;
site_dirs = {'1类场地', '2类场地', '3类场地', '4类场地'};
for i = 1:length(site_dirs)
site_path = site_dirs{i};
files = dir(fullfile(site_path, '*.txt'));
for j = 1:length(files)
file_path = fullfile(site_path, files(j).name);
acc = load(file_path);
acc = acc(:).'.*g;
n = length(acc);
Sa_matrix = zeros(length(damping_ratios), length(T));
Sv_matrix = zeros(length(damping_ratios), length(T));
Sd_matrix = zeros(length(damping_ratios), length(T));
for k = 1:length(damping_ratios)
xi = damping_ratios(k);
Sa = zeros(1, length(T));
Sv = zeros(1, length(T));
Sd = zeros(1, length(T));
for t = 1:length(T)
wn = 2 * pi / T(t);
Nfft = 2^nextpow2(n);
omega = 2 * pi * (0:Nfft-1) / (Nfft * dt);
af = fft(acc, Nfft);
H = 1 ./ (-(omega.^2) + 2i * xi * omega * wn + wn^2);
u = real(ifft(af .* H));
u = u(1:n);
Sd(t) = max(abs(u));
v = real(ifft(af .* H .* 1i .* omega));
v = v(1:n);
Sv(t) = max(abs(v));
a_rel = real(ifft(-af .* omega.^2 .* H));
a_rel = a_rel(1:n);
a_abs = a_rel + acc;
Sa(t) = max(abs(a_abs)) / g;
end
Sd_matrix(k, :) = Sd;
Sv_matrix(k, :) = Sv;
Sa_matrix(k, :) = Sa;
end
figure('Name', ['Sa - ', files(j).name], 'NumberTitle', 'off');
hold on; grid on;
colors = lines(length(damping_ratios));
for k = 1:length(damping_ratios)
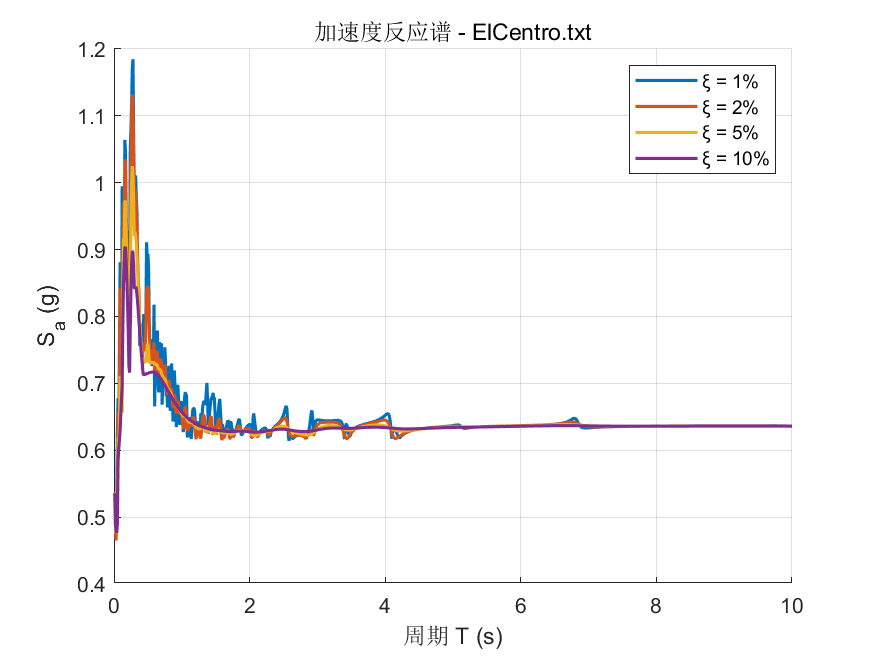
plot(T, Sa_matrix(k, :), 'DisplayName', ['ξ = ', num2str(damping_ratios(k)*100), '%'], ...
'Color', colors(k, :), 'LineWidth', 1.5);
end
xlabel('周期 T (s)'); ylabel('S_a (g)');
title(['加速度反应谱 - ', files(j).name]);
legend show; xlim([0 10]); ylim auto;
saveas(gcf, fullfile(site_path, [files(j).name(1:end-4), '_Sa.png']));
close;
figure('Name', ['Sv - ', files(j).name], 'NumberTitle', 'off');
hold on; grid on;
for k = 1:length(damping_ratios)
plot(T, Sv_matrix(k, :), 'DisplayName', ['ξ = ', num2str(damping_ratios(k)*100), '%'], ...
'Color', colors(k, :), 'LineWidth', 1.5);
end
xlabel('周期 T (s)'); ylabel('S_v (m/s)');
title(['速度反应谱 - ', files(j).name]);
legend show; xlim([0 10]); ylim auto;
saveas(gcf, fullfile(site_path, [files(j).name(1:end-4), '_Sv.png']));
close;
figure('Name', ['Sd - ', files(j).name], 'NumberTitle', 'off');
hold on; grid on;
for k = 1:length(damping_ratios)
plot(T, Sd_matrix(k, :), 'DisplayName', ['ξ = ', num2str(damping_ratios(k)*100), '%'], ...
'Color', colors(k, :), 'LineWidth', 1.5);
end
xlabel('周期 T (s)'); ylabel('S_d (m)');
title(['位移反应谱 - ', files(j).name]);
legend show; xlim([0 10]); ylim auto;
saveas(gcf, fullfile(site_path, [files(j).name(1:end-4), '_Sd.png']));
close;
end
end
|